Tabung merupakan bangun 3 dimensi (3D), artinya bangun tersebut dibatasi oleh tiga sisi yaitu sisi panjang, sisi lebar, dan sisi tinggi. Bangun yang memiliki panjang, lebar, dan tinggi pasti memiliki ruang/volume. Pada kesempatan ini kita akan belajar rumus mencari volume tabung. Selanjutnya dikembangkan lagi dengan mencari tinggi tabung, jari-jari tabung, dan diameter tabung.
Sebelum menghitung volume tabung, kita harus mengenal unsur-unsur pembentuk bangun ruang tabung. Tabung disusun dari 2 lingkaran yang sama luas dan dihubungkan dengan sebuah persegi atau persegi panjang yang disusun mengelilingi lingkaran. Volume tabung dihitung berdasarkan luas lingkaran dikalikan dengan tingginya.
Rumus Dasar Volume
Dalam menghitung volume bangun ruang dengan bentuk alas dan tutupnya sama selalu menggunakan rumus:

Jadi untuk menghitung volume kita harus mengetahui luas alas dan tingginya. Pengembangan pada rumus tersebut bergantung pada bentuk alasnya. Kita sering menjumpai alas bangun ruang berbentuk lingkaran, persegi, persegi panjang, maupun segitiga. Bentuk alas yang berbeda ini menyebabkan perubahan rumus pada luas alasnya.
Rumus Luas Lingkaran
Tabung memiliki alas berbentuk lingkaran. Untuk mencari luas lingkaran kita harus mengenal beberapa istilah yaitu pi (\(\pi\)), jari-jari (r), dan diameter (d).
Pi (\(\pi\)) adalah perbandingan antara keliling lingkaran dengan diameter lingkaran. Pi (\(\pi\)) yang digunakan adalah \(\frac{22}{7}\) artinya sebuah lingkaran dengan keliling 22 cm akan memiliki diameter 7 cm.
Selain menggunakan \(\frac{22}{7}\) alternatif berikutnya yaitu 3,14. 3,14 digunakan jika jari-jari, diameter, maupun tinggi tabung terlalu sulit untuk dibagi dengan 7.
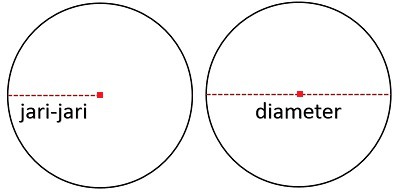
Jari-jari (r) adalah jarak antara sisi lingkaran dengan titik tengahnya. Jari-jari dapat diartikan setengah diameter (\(\frac{1}{2}\) x diameter).
Diameter (d) adalah jarak antara sisi lingkaran melewati titik tengah kemudian menuju sisi lingkaran. Diameter dapat diartikan dua kali jari-jari (2 x jari-jari).

Rumus Volume Tabung
Setelah diperoleh rumus luas lingkaran di atas, maka kita hanya perlu menambahkan dengan tingginya. Sehingga rumus volume tabung adalah

keterangan:
(\(\pi\)) = \(\frac{22}{7}\) atau 3,14
r = panjang jari-jari
t = tinggi tabung
Dari rumus tersebut selain digunakan untuk mencari volume tabung, juga dapat digunakan untuk menghitung panjang jari-jari, diameter, maupun tingginya. Untuk dapat memahami penggunaan rumus dalam mencari setiap unsur dari tabung, perhatikan contoh soal berikut!
Contoh Soal
Menghitung Volume dengan Rumus Tabung
1. Hitunglah volume tabung yang memiliki jari-jari alas 14 cm dan tinggi 10 cm!
Diketahui:
r = 14 cm
t = 10 cm
\(\pi\) = \(\frac{22}{7}\)
Jawab:
Volume tabung = \(\pi\) x r x r x t
= \(\frac{22}{7}\) x 14 x 14 x 10
= 6.160 cm \(^3\)
Jadi volume tabung tersebut adalah 6.160 cm \(^3\).
2. Hitunglah volume tabung yang memiliki diameter 20 cm dan tinggi 15 cm!
Diketahui:
r = 20 : 2 = 10 cm
t = 15 cm
\(\pi\) = 3,14
Jawab:
Volume tabung = \(\pi\) x r x r x t
= 3,14 x 10 x 10 x 15
= 4.710 cm \(^3\)
Jadi volume tabung tersebut adalah 4.710 cm \(^3\).
Menghitung Tinggi dengan Rumus Tabung
1. Hitunglah tinggi tabung yang memiliki jari-jari alas 14 cm dan volume 6.160 cm \(^3\)!
Diketahui:
r = 14 cm
v = 6.160 cm \(^3\)
\(\pi\) = \(\frac{22}{7}\)
Jawab:
Volume tabung = \(\pi\) x r x r x t
6.160 = \(\frac{22}{7}\) x 14 x 14 x t
6.160 = \(\frac{22}{7}\) x 196 x t
6.160 = \(\frac{4.312}{7}\) x t
6.160 = 616 x t
6.160 : 616 = t
10 = t
Jadi tinggi tabung tersebut adalah 10 cm.
2. Hitunglah tinggi tabung yang memiliki diameter 20 cm dan volume 4.710 cm \(^3\)!
Diketahui:
r = 20 : 2 = 10 cm
v = 4.710 cm \(^3\)
\(\pi\) = 3,14
Jawab:
Volume tabung = \(\pi\) x r x r x t
4.710 = 3,14 x 10 x 10 x t
4.710 = 314 x t
4.710 : 314 = t
15 = t
Jadi tinggi tabung tersebut adalah 15 cm.
Menghitung Jari-Jari dan Diameter
1. Hitunglah jari-jari dan diameter tabung yang memiliki volume 6.160 cm \(^3\) dan tinggi 10 cm!
Diketahui:
v = 6.160 cm \(^3\)
t = 10 cm
\(\pi\) = \(\frac{22}{7}\)
Jawab:
Volume tabung = \(\pi\) x r x r x t
6.160 = \(\frac{22}{7}\) x r x r x 10
6.160 = \(\frac{220}{7}\) x r x r
6.160 : \(\frac{220}{7}\) = r x r
6.160 x \(\frac{7}{220}\) = r x r
\(\frac{43.120}{220}\) = r x r
196 = r x r
\(\sqrt{196}\) = r
14 = r
Jadi jari-jari tabung tersebut adalah 14 cm dan diameternya adalah 14 cm x 2 = 24 cm.
Untuk dapat memahami perkalian dan pembagian yang melibatkan pecahan dapat dipelajari pada halaman Perkalian dan Pembagian Pecahan.
2. Hitunglah jari-jari dan diameter tabung yang memiliki volume 4.710 cm \(^3\) dan tinggi 15 cm!
Diketahui:
v = 4.710 cm \(^3\)
t = 15 cm
\(\pi\) = 3,14
Jawab:
Volume tabung = \(\pi\) x r x r x t
4.710 = 3,14 x r x r x 15
4.710 = 47,1 x r x r
\(\frac{4.710}{47,1}\) = r x r
100 = r x r
\(\sqrt{100}\) = r
10 = r
Jadi jari-jari tabung tersebut adalah 10 cm dan diameternya adalah 10 cm x 2 = 20 cm.
Baca: Kumpulan Soal Cerita Tabung Dilengkapi Pembahasan
Untuk mengetahui cara menyelesaikan akar kuadrat dari contoh soal mencari jari-jari di atas dapat memperhatikan video berikut!









Kk
Kalau mencari jari jari sebuah tabung yg hanya di ketahui p×l selimut tabung nya
Hitungnya gimana ya kk
To long batu y kk
bagian panjang atau lebar yang mengelilingi alas lingkarannya?
jika panjang yang dianggap mengelilingi alas lingkarannya maka panjang itu bisa disebut juga dengan keliling lingkaran.
Keliling = phi x diameter
dicari diameternya kemudian dari diameter tersebut dibagi 2 maka ditemukan jari-jari
semoga bisa membantu 🙂