Lingkaran merupakan bangun datar yang memiliki satu sisi dan tidak memiliki sudut maupun titik sudut. Karena bentuknya yang unik maka lingkaran memiliki simetri lipat, sumbu simetri, dan simetri putar yang tak terhingga. Pada halaman ini kita akan mempelajari bagaimana rumus luas dan keliling lingkaran dapat terbentuk.
Ciri-Ciri Lingkaran
Lingkaran memiliki ciri-ciri khusus yang membedakan dengan bangun datar lainnya. Ciri-ciri tersebut diantaranya:
- Lingkaran tidak memiliki sudut maupun titik sudut,
- Lingkaran hanya memiliki 1 sisi,
- Lingkaran memiliki simetri lipat, sumbu simetri, dan simetri putar tak terhingga.
Unsur-Unsur Lingkaran
1. Pi (\(\pi\))
Pi (\(\pi\)) adalah perbandingan antara keliling lingkaran dengan diameter lingkaran. Bilangan bulat yang paling kecil yang mampu menggambarkan perbandingan keliling lingkaran dan diameter lingkaran adalah 22 dan 7. Artinya jika sebuah lingkaran memiliki keliling 22 maka diameternya tepat 7. Sehingga pi (\(\pi\)) yang digunakan adalah \(\frac{22}{7}\) artinya sebuah lingkaran dengan keliling 22 akan memiliki diameter 7.
Penggunaan \(\frac{22}{7}\) pada penghitungan luas dan keliling lebih diutamakan. Tetapi jika jari-jari maupun diameter lingkaran tidak bisa tepat dibagi tujuh, maka digunakan alternatif 3,14.

2. Diameter (d)
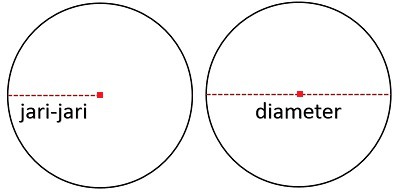
Pada pi (\(\pi\)) disebutkan salah satu pembandingnya merupakan diameter. Diameter adalah jarak antara sisi lingkaran dengan titik pusat lingkaran kembali lagi ke sisi lingkaran, biasa juga dikenal dengan dua kali jari-jari.
3. Jari-Jari (r)
Jari-jari (r) adalah jarak antara sisi lingkaran dengan titik pusat lingkaran.
4. Titik Pusat
Titik pusat adalah titik tengah lingkaran yang mempunyai jarak yang sama keberbagai sisi lingkaran.
Baca: Menghitung Volume Tabung
Rumus Lingkaran
1. Rumus Luas Lingkaran

Rumus luas lingkaran diperoleh dari pi (\(\pi\)) dikalikan dengan jari-jari (r) dan dikalikan dengan jari-jari lagi (r).
2. Rumus Keliling Lingkaran

Rumus keliling lingkaran diperoleh dari pi (\(\pi\)) dikali dengan diameter lingkaran.
Contoh soal
1. Sebuah lingkaran memiliki panjang jari-jari 14 cm. Luas dan keliling lingkaran tersebut masing-masing adalah … dan ….
Jawab:
Luas lingkaran = \(\pi\) x r x r
= \(\frac{22}{7}\) x 14 x 14
= 616 cm\(^2\)
2. Sebuah lingkaran memiliki panjang diameter 20 cm. Luas dan keliling lingkaran tersebut masing-masing adalah … dan ….
Jawab:
Jari-jari = diameter : 2
= 20 : 2
= 10 cm
Luas lingkaran = \(\pi\) x r x r
= 3,14 x 10 x 10
= 314 cm\(^2\)
3. Sebuah lingkaran memiliki luas 154 cm\(^2\). Panjang jari-jari dan diameter lingkaran tersebut masing-masing adalah … dan ….
Jawab:
Luas lingkaran = \(\pi\) x r x r
154 = \(\frac{22}{7}\) x r x r
154 : \(\frac{22}{7}\) = r x r
154 x \(\frac{7}{22}\) = r x r
49 = r x r
\(\sqrt{49}\) = r
7 = r


![Rumus Volume, Tinggi, dan Jari-Jari Tabung [Lengkap] menghitung volume tabung](https://kependidikan.com/wp-content/uploads/2019/10/rumus-volume-tabung-1-218x150.jpg)