Pernahkah kamu mendengar rumus pythagoras? Rumus pythagoras digunakan untuk menghitung panjang sisi miring segitiga. Rumus ini diberi nama sesuai dengan nama penemunya yaitu Pythagoras. Pythagoras adalah seorang matematikawan dan filsuf Yunani yang paling dikenal melalui teorema pythagoras.
Segitiga yang dikenal yaitu segitiga sama sisi, segitiga sama kaki, segitiga sembarang, dan segitiga siku-siku. Teori pythagoras dapat berlaku untuk menghitung sisi miring pada segitiga siku-siku.
Rumus Pythagoras
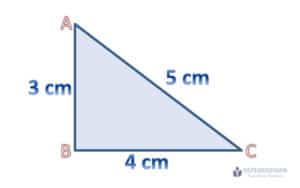 Dalam teori pythagoras, kuadrat sisi miring segitiga siku-siku merupakan jumlah kuadrat kedua sisi lainnya. Segitiga siku-siku memiliki 3 sisi yaitu sisi tegak (AB), sisi lurus (BC), dan sisi miring (AC).
Dalam teori pythagoras, kuadrat sisi miring segitiga siku-siku merupakan jumlah kuadrat kedua sisi lainnya. Segitiga siku-siku memiliki 3 sisi yaitu sisi tegak (AB), sisi lurus (BC), dan sisi miring (AC).
Rumus Sisi Miring
Dalam matematika, teori pythagoras diatas dapat dinyatakan sebagai berikut:
AC\(^2\) = AB\(^2\) + BC\(^2\)
Jika diterapkan pada gambar segitiga siku-siku di atas maka ditulis sebagai berikut
AC\(^2\) = AB\(^2\) + BC\(^2\)
AC\(^2\) = 3\(^2\) + 4\(^2\)
AC\(^2\) = 9 + 16
AC\(^2\) = 25
AC = \(\sqrt[]{25}\)
AC = 5
Jadi panjang sisi miring adalah 5 cm.
Selain digunakan untuk menghitung panjang sisi miring. Rumus di atas juga dapat disesuaikan untuk menghitung sisi tegak dan sisi datar. Dari rumus di atas, dapat dikembangkan lagi menjadi 2 rumus yaitu:
Rumus Sisi Tegak
AB\(^2\) = AC\(^2\) – BC\(^2\)
Jika diterapkan pada gambar segitiga siku-siku di atas maka ditulis sebagai berikut
AB\(^2\) = AC\(^2\) – BC\(^2\)
AB\(^2\) = 5\(^2\) – 4\(^2\)
AB\(^2\) = 25 + 16
AB\(^2\) = 9
AB = \(\sqrt[]{9}\)
AB = 3
Jadi panjang sisi tegak dari segitiga siku-siku di atas adalah 3 cm.
Rumus Sisi Datar
BC\(^2\) = AC\(^2\) – AB\(^2\)
Jika diterapkan pada gambar segitiga siku-siku di atas maka ditulis sebagai berikut
BC\(^2\) = AC\(^2\) – AB\(^2\)
BC\(^2\) = 5\(^2\) – 3\(^2\)
BC\(^2\) = 25 + 9
BC\(^2\) = 16
BC = \(\sqrt[]{16}\)
BC = 4
Jadi panjang sisi datar dari segitiga siku-siku di atas adalah 4 cm.
Baca juga: Ciri-Ciri Persegi Panjang
Triple Pythagoras
Triple pythagoras adalah kombinasi 3 bilangan yang sesuai dengan teori pythagoras. Berikut ini daftar triple pythagoras yang umum digunakan dalam soal
| AB | BC | AC |
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 40 | 41 |
| 11 | 60 | 61 |
| 12 | 35 | 37 |
| 13 | 84 | 85 |
| 16 | 63 | 65 |
| 20 | 21 | 29 |
| 28 | 45 | 53 |
| 33 | 56 | 65 |
| 36 | 77 | 85 |
| 39 | 80 | 89 |
| 48 | 55 | 73 |
| 65 | 72 | 97 |
Kombinasi bilangan-bilangan di atas berlaku pula kelipatannya. Misalnya kombinasi 3, 4, 5 bisa dikembangkan menjadi 6, 8, 10 dan seterusnya.
Demikian pembahasan tentang rumus pythagoras. Semoga meningkatkan pemahaman tentang menghitung sisi-sisi pada segitiga siku-siku. Pertanyaan dan masukkan silahkan dituliskan dalam kolom komentar di bawah.










